R Objects

Learning objectives

In this section, you will learn

• how to store objects (think of variables, functions, datasets) into the R workspace (think of the place where R stores all its objects)
• how to use the stored objects

An example: repayment of loans

Let’s start with a simple example.

Suppose you want to know how much you will have to pay to the bank if you borrow an amount $L$ and you intend to reimburse a fixed amount over a period of $N$ months, and the bank intend to charge you an annual interest rate $r$.

There are different ways to consider this problem, but for this example we will use the textbook formula:

$$ m = L . \frac{(\frac{r}{1200})(1 +\frac{r}{1200})^N}{(1+ \frac{r}{1200})^N -1 } $$

One advantage of a programming language is that we can define variables and keep such expressions general. So, if we are asked to answer this question when borrowing 2000 for 24 months at an interest of 6% per year, we can define $L$ as $10000$, $N$ as $24$, and $r$ as $6$.

First, we will launch the R programme we have just installed (for example, by clicking at the R icon present in your desktop).

In R, we can declare variables using the assignment symbol <-, which is the “less than” sign followed by a minus. Note that it looks like a little arrow. L <- 10000 means that you’re assigning the number 10000 to the variable named L.

Note: We could also use = the equals sign for assignment. Both are correct, but we tend to prefer the “<-” assignement.

Try it out in your console.

# let's declare three variables and assign them initial values
L <- 10000
N <- 24
r <- 6

Note that R did not print anything out when you made these assignments.

Had you made a mistake, you would have received an error message. For example, if you forgot the minus sign to make a complete arrow and get the assignment right, you will receive an error message. For example, try this:

 u < 24

## Error in eval(expr, envir, enclos): object 'u' not found

Once it is stored, you can see the value stored in a variable by typing its name in in the console.

# what value is stored in the variable L
L

## [1] 10000

And when we hit the Return key, R shows us the value stored in $L$, which is $10000$.

As we define objects in the console, we are actually changing what is called the workspace.

You can see all the variables saved in your workspace by typing ls().

ls is a predefined R function that shows you the names of the objects saved in your workspace. By predefined, we mean that you can use them without having to load any additional package, or to define them by yourself.

Just type it in your console:

ls()

## [1] "L" "N" "r"

Since the problem parameters are saved in variables, to obtain a solution, we can use the variables directly.

To be able to calculate the formula, we will again rely on R predefined operators / ,^ , and *.

# Enter the formula using the variables
L * (r/1200) *(1+r/1200)^N / ((1 + r/1200)^N - 1) 

## [1] 443.2061

Note that simply typing the formula with the variables gives you the solution, but does not store it into the workspace. If you want to use the solutions obtained for further calculations, you need to assign them to a new variable.

# Calculate the formula and store it in a new variable m
m <- L * (r/1200) *(1+r/1200)^N / ((1 + r/1200)^N - 1) 

Again the solutions are not printed out to your console, but they are stored in the workspace and ready to be used for further work. If you want to see the variable, you have to type it on another line and press CTRL + Enter keys.

m 

## [1] 443.2061

L <- 20000
m

## [1] 443.2061

As a small trick, if you want to store the value to the workspace and at the same time see the result on the console, you can surround your assignment with brackets:

# Surround assignments with brackets to see print the results of the assignment
# We reassign the value of 10000 to L
L <- 10000
(m <- L * (r/1200) *(1+r/1200)^N / ((1 + r/1200)^N - 1))

## [1] 443.2061

(extra <-  (m * N) - L )

## [1] 636.9465

In any case, if you did things correctly you should get 443.2061025 to be paid per month, and paid an extra 636.9464607 to your banker to get access to that money immediately !

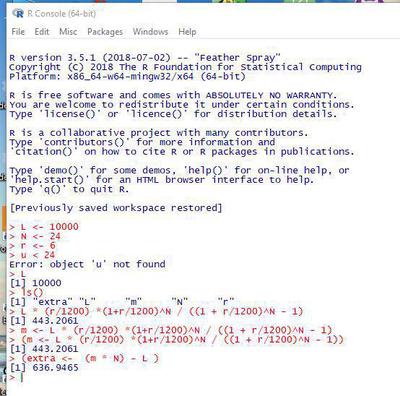
The Figure 1 shows how your console should look like at the end of this session if you followed all the instructions.

Video of this section

Additional resources

There are many resources available over the internet. Here we suggest two specific pages of the Tutorialpoints website that are giving more details about the names of variables, and the predefined operators R.

• More on R variable names
• More on R operators

Exercises

Ex. 1: Play with variables

• Create two new variables \(i\) and \(j\) and assign them the values 1 and 2 respectively
• Create a new variable sinij that stores the value of sinus of the sum of i and j (tips: browse the internet to figure out how the sinus function is defined in base R)
• Display the variable sinij on your console

i <- 1
j <- 2
(sinij <- sin(i+j))

## [1] 0.14112

Ex. 2: Add the first 100 integers.

We know that the sum of the first \(n\) integers is given by the formula \(\frac{n (n+1)}{2}\)

• Create a variable \(n\) and assign the value 10
• Calculate the sum of the 10 first integers and store it in a variable s10
• Calculate the sum of the 100 first integers
• You can see that this exercise can be repetitive and it will be useful to develop a specific function that would avoid repetitions.

n <- 10
s10 <- n * (n+1)/2
s10

## [1] 55

n2 <- 100
s100 <- n2 * (n2+1)/2
s100

## [1] 5050